Input Parameters
Results & Visualization
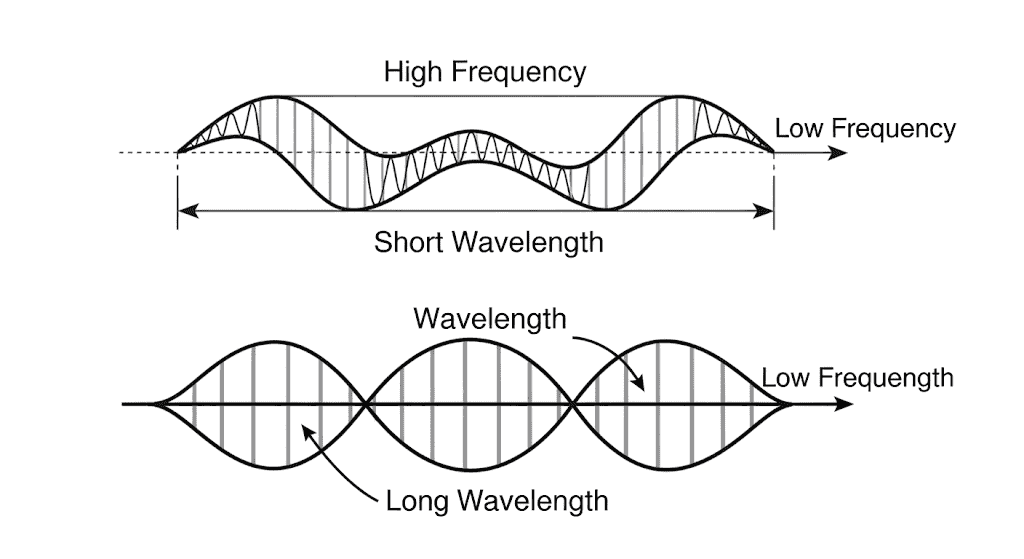
What is Wavelength?
Wavelength represents the distance between two consecutive peaks or troughs of a wave as it travels through a medium. In physics and engineering, wavelength serves as a fundamental parameter that determines wave behavior across electromagnetic radiation, sound waves, and fluid dynamics applications.
The wavelength entity contains several critical attributes that define its practical applications:
| Entity | Attribute | Value Examples |
|---|---|---|
| Wavelength | Unit | meters (m), nanometers (nm), centimeters (cm), micrometers (μm) |
| Wavelength | Domain | Electromagnetic radiation, acoustics, fluid dynamics |
| Wavelength | Application | Radio communication, optics, medical imaging, sonar |
| Wavelength | Dependence | Speed of propagation, frequency |
| Wavelength | Related Formula | λ = v / f |
Wavelength measurements vary dramatically across different wave types. Visible light wavelengths span 380-700 nanometers, while radio waves extend from millimeters to kilometers. Sound wavelengths in air at room temperature range from centimeters for high-frequency sounds to meters for low-frequency vibrations.
The wavelength-frequency relationship forms an inverse proportional connection. Higher frequency waves compress into shorter wavelengths, while lower frequency waves stretch across longer distances. This relationship remains constant for waves traveling through the same medium at consistent speeds.
How to Calculate Wavelength
The good news is that you don’t need to be a physics genius to calculate wavelength. The formula is beautifully simple:
λ=fv
Let’s break that down:
- lambda (Wavelength): This is what you want to find.
- v (Wave Speed): This is how fast the wave is traveling through a medium (like air, water, or a vacuum).
- f (Frequency): This is how many wave cycles pass a point each second. Its unit is Hertz (Hz).
Key to Accuracy: Use the Right Units!
For the formula to work correctly, your units need to be compatible. The standard is:
- Speed in meters per second (m/s)
- Frequency in Hertz (Hz)
- The resulting wavelength will be in meters (m)
If your frequency is in kilohertz (kHz), megahertz (MHz), or gigahertz (GHz), you’ll need to convert it to Hz first.
| Frequency Unit | Conversion to Hertz (Hz) |
| 1 Kilohertz (kHz) | 1,000 Hz |
| 1 Megahertz (MHz) | 1,000,000 Hz |
| 1 Gigahertz (GHz) | 1,000,000,000 Hz |
This single formula works for almost any wave you can think of, from the light from a distant star to the sound of a guitar string.
Unit Compatibility Requirements
Successful wavelength calculations require consistent unit alignment:
| Wave Speed Units | Frequency Units | Resulting Wavelength Units |
|---|---|---|
| m/s | Hz | meters (m) |
| km/s | kHz | meters (m) |
| m/s | MHz | micrometers (μm) |
| mm/s | Hz | millimeters (mm) |
Converting between frequency units prevents calculation errors. One kilohertz equals 1,000 Hz, while one megahertz equals 1,000,000 Hz. Speed conversions follow similar patterns: 1 km/s equals 1,000 m/s.
Application Contexts
Wavelength calculations serve diverse scientific and engineering applications:
Electromagnetic Waves: Radio frequency design, antenna optimization, microwave engineering, optical fiber communications, and satellite signal propagation rely on precise wavelength measurements.
Sound Waves: Acoustic engineering, noise control, architectural acoustics, and audio equipment design utilize wavelength calculations to optimize sound transmission and reception.
Water Waves: Ocean engineering, coastal protection, ship design, and marine navigation systems depend on wave wavelength analysis for structural integrity and safety planning.
Wavelength Calculator Tool
The wavelength calculator streamlines complex wave calculations through an intuitive interface that accepts frequency and speed inputs to generate precise wavelength outputs. Users input wave frequency values in Hz, kHz, or MHz units alongside propagation speed measurements in appropriate units.
Input Parameters
Frequency Input: The calculator accepts frequency values across the electromagnetic spectrum, from extremely low frequency (ELF) waves at 3-30 Hz to extremely high frequency (EHF) waves reaching 300 GHz. Input validation ensures numerical accuracy and prevents calculation errors.
Speed Input: Wave speed values adapt to the propagation medium. Light speed (299,792,458 m/s) applies to electromagnetic waves in vacuum, while material-specific speeds accommodate other wave types. The calculator includes preset values for common media.
Output Features
Real-time Calculation: The calculator processes inputs instantaneously, displaying wavelength results as users modify frequency or speed values. This dynamic response enables rapid parameter exploration and optimization.
Unit Conversion: Automatic unit conversion displays results in meters, centimeters, millimeters, micrometers, and nanometers, accommodating different application requirements. Users select preferred output units based on their specific needs.
Precision Control: The calculator maintains scientific accuracy with configurable decimal precision, supporting both engineering approximations and research-grade calculations.
Real-World Examples of Wavelength Calculation
1. The Color of Light
The color of the light we see is determined by its wavelength. Let’s find the wavelength of green light.
| Parameter | Value |
| Context | Visible Light |
| Wave Speed (v) | 299,792,458 m/s (the speed of light) |
| Frequency (f) | 560 THz (5.6times1014 Hz) |
| Result (lambda) | ~535 nanometers |
This tiny wavelength falls right in the green portion of the visible light spectrum.
2. Your Wi-Fi Signal
Your Wi-Fi router uses radio waves to send data. Let’s calculate the wavelength of a standard 2.4 GHz signal.
| Parameter | Value |
| Context | Wi-Fi Radio Wave |
| Wave Speed (v) | 299,792,458 m/s (travels at the speed of light) |
| Frequency (f) | 2.4 GHz (2.4times109 Hz) |
| Result (lambda) | 12.5 centimeters (or about 4.9 inches) |
This is why the antennas on routers and devices are just a few inches long—they are sized to efficiently interact with this wavelength!
3.Sound Wave Propagation in Air
A 1000 Hz sound wave traveling through air at 20°C (343 m/s) produces a wavelength of:
λ = 343 m/s ÷ 1000 Hz = 0.343 m = 34.3 cm
This wavelength measurement influences speaker design, room acoustics, and noise control strategies. Sound waves with wavelengths comparable to room dimensions create standing wave patterns that affect audio quality.
4.Radio Wave Communication
An FM radio station broadcasting at 100 MHz generates electromagnetic waves with wavelengths of:
λ = 299,792,458 m/s ÷ 100,000,000 Hz = 2.998 m ≈ 3 meters
This wavelength determines antenna design requirements, signal propagation characteristics, and coverage area limitations. Radio engineers use these calculations to optimize transmission efficiency and minimize interference.
5.Fiber Optic Communications
Infrared light at 1550 nm wavelength (1.93 × 10^14 Hz) traveling through optical fiber demonstrates telecommunications applications:
λ = 299,792,458 m/s ÷ 1.93 × 10^14 Hz = 1.55 × 10^-6 m = 1550 nm
This wavelength represents the optimal transmission window for long-distance fiber optic communications, minimizing signal loss and maximizing data transmission rates.
6.Medical Ultrasound Applications
Diagnostic ultrasound at 5 MHz frequency traveling through human tissue at approximately 1540 m/s produces:
λ = 1540 m/s ÷ 5,000,000 Hz = 0.000308 m = 0.308 mm
This wavelength enables high-resolution medical imaging while maintaining safe tissue penetration depths. Medical professionals use these calculations to optimize imaging quality and diagnostic accuracy.
Wavelength vs Frequency vs Speed – How Are They Related?
The wavelength-frequency-speed relationship forms the foundation of wave physics, connecting three fundamental wave properties through mathematical precision. This relationship maintains consistency across all wave types while adapting to different propagation media.
Fundamental Relationships
| Wave Property | Definition | Units | Relationship |
|---|---|---|---|
| Wavelength (λ) | Distance between wave peaks | meters | λ = v / f |
| Frequency (f) | Wave cycles per second | Hertz (Hz) | f = v / λ |
| Speed (v) | Wave propagation velocity | meters/second | v = f × λ |
Inverse Proportionality Principle
Wavelength and frequency maintain an inverse proportional relationship when wave speed remains constant. As frequency increases, wavelength decreases proportionally. This relationship enables wave tuning and frequency selection across communication systems.
Mathematical Expression: λ₁ × f₁ = λ₂ × f₂ (constant speed)
Medium-Dependent Speed Variations
Wave speed changes dramatically across different propagation media, affecting wavelength calculations while frequency remains constant:
| Medium | Wave Type | Speed (m/s) | Example Frequency | Resulting Wavelength |
|---|---|---|---|---|
| Vacuum | Electromagnetic | 299,792,458 | 1 GHz | 0.3 m |
| Air (20°C) | Sound | 343 | 1000 Hz | 0.343 m |
| Water | Sound | 1482 | 1000 Hz | 1.482 m |
| Glass | Light | 200,000,000 | 5×10^14 Hz | 400 nm |
Practical Implications
The wavelength-frequency-speed relationship drives engineering decisions across multiple disciplines. Antenna designers select lengths based on operating frequency wavelengths. Audio engineers consider room dimensions relative to sound wavelengths. Optical engineers optimize fiber specifications using light wavelength characteristics.
FAQs About Wavelength Calculations
What is the unit of wavelength?
Wavelength measurements use distance units appropriate to the wave scale. Meters serve as the standard SI unit, while nanometers accommodate optical applications, and kilometers suit radio wave analysis. Unit selection depends on practical measurement convenience and application requirements.
Why is wavelength important in communication?
Communication systems rely on wavelength parameters for antenna design, signal propagation modeling, and interference analysis. Antenna efficiency peaks when physical dimensions match specific wavelength fractions. Signal propagation characteristics change with wavelength, affecting coverage areas and transmission quality.
How does temperature affect sound wavelength?
Temperature variations alter sound speed in air, directly impacting wavelength calculations. Sound speed increases approximately 0.6 m/s per degree Celsius temperature rise.
Higher temperatures expand air molecules, facilitating faster sound transmission and longer wavelengths at constant frequency.Check out this resource from Penn State University for more details.
| Temperature (°C) | Sound Speed (m/s) | 1000 Hz Wavelength |
|---|---|---|
| 0 | 331.3 | 0.331 m |
| 20 | 343.2 | 0.343 m |
| 40 | 355.1 | 0.355 m |
Is wavelength used in radar and sonar?
Radar and sonar systems depend heavily on wavelength calculations for target detection, range measurement, and resolution optimization. Shorter wavelengths provide higher resolution but reduced penetration range. Longer wavelengths offer deeper penetration with lower resolution capabilities.
Radar wavelength selection balances detection range against resolution requirements. Weather radar uses longer wavelengths to penetrate storm systems, while precision tracking radar employs shorter wavelengths for accurate position determination.
Wavelength Applications in Different Fields
Physics and Electromagnetic Spectrum
Wavelength classification organizes electromagnetic radiation into distinct regions based on wavelength ranges. This organization enables scientific understanding and practical applications across the electromagnetic spectrum.
| Radiation Type | Wavelength Range | Applications |
|---|---|---|
| Radio Waves | 1 mm – 100 km | Broadcasting, telecommunications |
| Microwaves | 1 mm – 1 m | Satellite communication, radar |
| Infrared | 700 nm – 1 mm | Thermal imaging, fiber optics |
| Visible Light | 380 nm – 700 nm | Human vision, photography |
| Ultraviolet | 10 nm – 380 nm | Sterilization, fluorescence |
| X-rays | 0.01 nm – 10 nm | Medical imaging, crystallography |
Engineering and Communication Systems
Radio frequency engineering utilizes wavelength calculations for antenna design, transmission line optimization, and signal propagation analysis.
Quarter-wave and half-wave antenna configurations achieve optimal radiation efficiency through precise wavelength matching.
Microwave engineering applies wavelength principles in waveguide design, cavity resonator development, and radar system optimization. Component dimensions correlate directly with operating wavelength requirements for maximum performance.
Medical and Healthcare Applications
Medical imaging technologies rely on wavelength selection for optimal tissue penetration and resolution. Ultrasound wavelengths determine imaging depth and clarity, while X-ray wavelengths enable bone and tissue visualization.
Therapeutic applications utilize specific wavelengths for targeted treatment delivery. Laser therapy employs precise wavelength selection for tissue interaction control, while photodynamic therapy uses wavelength-specific light activation.
Marine and Underwater Applications
Sonar systems calculate wavelength parameters for underwater navigation, fish detection, and seafloor mapping. Low-frequency sonar uses longer wavelengths for deep-water penetration, while high-frequency sonar employs shorter wavelengths for detailed imaging.
Underwater communication systems adapt wavelength calculations to water’s acoustic properties. Sound wavelength variations with water temperature, salinity, and pressure affect communication range and clarity.
Conclusion
Wavelength calculations form the mathematical foundation for wave-based technologies across physics, engineering, and medical applications.
The fundamental relationship λ = v / f connects wave speed, frequency, and wavelength through precise mathematical principles that enable practical problem-solving across diverse fields.
The wavelength calculator tool simplifies complex calculations while maintaining scientific accuracy required for professional applications.
Real-time processing, unit conversion capabilities, and precision control features support both educational learning and engineering development requirements.
Modern communication systems, medical diagnostic equipment, and scientific instruments depend on accurate wavelength calculations for optimal performance.
The wavelength calculator tool bridges theoretical understanding with practical implementation, supporting innovation across wave-based technologies and applications.